Persiapan
Lulus CPNS

1.1 Pengertian Bangun Ruang

Bangun ruang adalah bangun matematika yang mempunyai isi atau Volume. Bangun ruang sering juga disebut bangun 3 dimensi karena memiliki 3 komponen utama sebagai berikut.
1.2 Bagian-bagian bangun ruang :

• Sisi               : bidang pada bangun ruang yang membatasi antara bangun ruang dengan ruangan sekitarnya  
• Rusuk           : pertemuan dua sisi yang berupa ruas garis pada bangun ruang        
• Titik sudut     : titik hasil pertemuan rusuk yang berjumlah tiga atau lebih.       

2 Jenis-Jenis Bangun Ruang yang umum dikenal adalah:

  1. Kubus

  2. Balok

  3. Prisma

  4. Limas

  5. Kerucut

  6. Tabung

  7. Bola

  3. Ciri–ciri,Rumus Bangun Ruang

   2.1 Kubus

    Merupakan bangun yang dibatasi oleh 6 sisi yang sama dan sebangun.

Ciri-ciri KUBUS, antara lain :

Ø  Kubus merupakan bangun ruang dengan 6 sisi sama besar (kongruen),

Ø  Kubus mempunyai 6 sisi berbentuk persegi,

Ø  Kubus mempunyai 12 rusuk yang sama panjang,

Ø  Kubus mempunyai 8 titik sudut,

Ø  Jaring-karing kubus berupa 6 buah persegi yang kongruen.

Rumus Luas Permukaan Kubus

L  =  6 x r²

        L  :  luas permukaan

        r  :  panjang rusuk

Rumus Volume Kubus

V  =  r³

        V  :  Volume

        r   :  panjang rusuk

   2.2 Balok

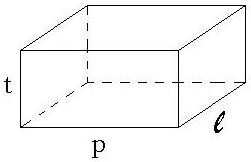
   Merupakan bangun yang dibatasi oleh 6 sisi yang mempunyai ukuran panjang dan lebar

Ciri-ciri BALOK,antara lain:

Ø  Balok merupakan bangun ruang yang dibatasi 6 persegi panjang dimana 3 persegi panjang kongruen,

Ø  Balok mempunyai 6 sisi berbentuk persegi panjang,

Ø  Balok mempunyai 3 pasang bidang sisi berhadapan yang kongruen,

Ø  Balok mempunyai 12 rusuk,

Ø  4 buah rusuk yang sejajar sama panjang,

Ø  Balok mempunyai 8 titik sudut,

Ø  Jaring-jaring balok berupa 6 buah persegi panjang.

Rumus Luas Permukaan Balok

L  =  2 x [(p x l) + (p x t) + (l x t)]

L   :  luas permukaan

p   :  panjang balok

l    :  lebar balok

t    :  tinggi balok

Rumus Volume Balok

V  =  p x l x t

      V     :  volume balok

      p     :  panjang balok

      l      :  lebar balok

      t      :  tinggi balok

    2.3 Prisma

    Merupakan bangun yang dibatasi oleh 6 sisi yang mempunyai ukuran panjang dan lebar

Ciri-ciri PRISMA, antara lain:

Ø  Prisma merupakan bangun ruang yang alas dan atasnya kongruen dan sejajar,

Ø  Rusuk prisma alas dan atas yang berhadapan sama dan sejajar,

Ø  Rusuk tegak prisma sama dan sejajar,

Ø  Rusuk tegak prisma tegak lurus dengan alas dan atas prisma,

Ø  Rusuk tegak prisma disebut juga tinggi prisma,

Ø  Prisma terdiri dari prisma segitiga dan prisma beraturan.

Ø  Prisma segitiga mempunyai bidang alas dan bidang atas berupa segitiga yang kongruen.

Ø  Prisma segitiga mempunyai 5 sisi.

Ø  Prisma segitiga mempunyai  9 rusuk

Ø  Prisma segitiga mempunyai 6 titik sudut

Ø  Jaring-jaring prisma segitiga berupa 2 segitiga, dan 3 persegi panjang.

Rumus Luas Permukaan Prisma Segitiga

L  =  Keliling ∆  x  t  x ( 2 x Luas ∆)

L          :  luas permukaan

∆          :  alas dan atas segitiga

t           :  tinggi prisma

Volume Prisma Segitiga

V  =  Luas Alas  x  t 

V               :  Volume

Luas Alas   :  Luas ∆   =  ( ½ a x t )

t               :  tinggi prisma

    2.4 Limas

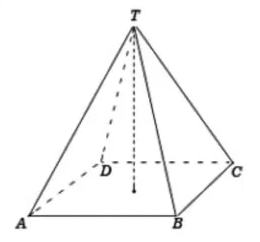
Merupakan bangun yang dibatasi oleh sisi yang berbentuk segitiga

Ciri-ciri LIMAS,antara lain:

Ø  Limas adalah bangun ruang yang mempunyai bidang alas segi banyak dan dari bidang alas tersebut dibentuk suatu sisi berbentuk segitiga yang akan bertemu pada satu titik,

Ø  Nama limas ditentukan oleh bentuk alasnya,

Ø  Limas beraturan yaitu limas yang alasnya berupa segi beraturan,

Rumus Luas Permukaan Limas

L =  luas alas + luas selubung limas

Rumus Volume Limas

V =   1/3 ( luas alas  x  t )

V         :  volume limas

t          :  tinggi limas

  2.5 Kerucut

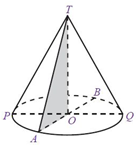
Merupakan bangun yang dibatasi oleh alas yang berbentuk lingkaran dan selimut yang berbentuk lengkung

Ciri-ciri KERUCUT,antara lain:

Ø  Kerucut merupakan bangun ruang berbentuk limas yang alasnya berupa lingkaran,

Ø  Kerucut mempunyai 2 sisi,

Ø  Kerucut tidak  mempunyai rusuk,

Ø  Kerucut mempunyai 1 titik sudut,

Ø  Jaring-jaring kerucut terdiri dari lingkaran dan segi tiga.

Rumus Luas Kerucut

L  =   π r² + π d x t

L     :  luas permukaan

r      :  jari-jari lingkaran alas

d     :  diameter lingkaran alas

t      :  tinggi kerucut

Rumus Volume Kerucut

V = 1/3  ( π r²  x  t )

V   :  volume

r    :  jari-jari lingkaran alas

t    :  tinggi kerucut

   2.6 Tabung

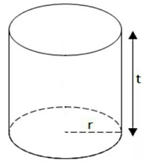
Merupakan bangun yang dibatasi oleh sisi lengkung dan buah lingkaran

Ciri-ciri TABUNG, antara lain:

Ø  Tabung merupakan bangun ruang berupa prisma tegak dengan bidang alas dan atas berupa lingkaran,

Ø  Tinggi tabung adalah jarak titik pusat bidang lingkaran alas dengan titik pusat lingkaran atas,

Ø  Bidang tegak tabung berupa lengkungan yang disebut selimut tabung,

Ø  Jaring-jaring tabung tabung berupa 2 buah lingkaran dan 1 persegi panjang.

Rumus Luas Permukaan Tabung

L  =  2 x ( π r² ) + π d x t

L    :  luas permukaan

r    :  jari-jari lingkaran alas

d   :  diameter lingkaran alas

t    :  tinggi tabung

Rumus Volume Tabung

V =  1/3  (luas alas x t)

V             :   Volume

luas alas  :  π r²

r              : jari-jari alas
t              : tinggi tabung

   2.7 Bola

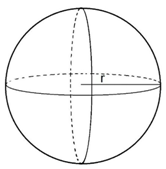
Merupakan bangun yang dibatasi oleh sisi lengkung

Ciri-ciri BOLA, antara lain:

Ø  Bola merupakan bangun ruang berbentuk setengah lingkaran diputar mengelilingi garis tengahnya,

Ø  Bola mempunyai 1 sisi dan 1 titik pusat,

Ø  Sisi bola disebut dinding bola,

Ø  Bola tidak mempunyai titik sudut dan rusuk,

Ø  Jarak dinding ke titik pusat bola disebut jari-jari,

Ø  Jarak dinding ke dinding dan melewati titik pusat disebut diameter.

Rumus Luas Permukaan Bola

L  =  4 π  r²

L    :  luas permukaan

r    :  jari-jari bola

Rumus Volume Bola

V  =  ⁴/₃  π r³

V     :  volume

r      : jari-jari bola