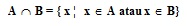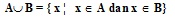Persiapan
Lulus CPNS

1. Pengertian Himpunan

Himpunan adalah kumpulan benda atau objek yang dapat didefinisikan dengan jelas. Benda atau objek dalam himpunan disebut elemen atau anggota himpunan. Dari definisi tersebut, dapat diketahui objek yang termasuk anggota himpunan atau bukan.

1.2 IRISAN dan GABUNGAN DUA HIMPUNAN

1. Irisan Dua Himpunan

Irisan dua himpunan A dan B adalah himpunan semua objek atau anggota himpunan yang sekaligus menjadi anggota himpunan A dan B. Adapun bentuk umum irisan adalah :

Contoh :

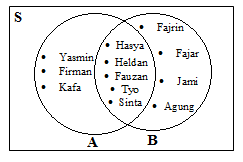
a.  A = {Hasya,Yasmin,Sinta,Fauzan,Heldan,Firman,Kafa,Tyo}

B = {Fajrin,Fajar,Jami,Hasya,Fauzan,Heldan,Tyo,Sinta,Agung}

Dari himpunan A dan B tersebut, terdapat anggota-anggota himpunan sdari kedua himpunan tersebut yang sama. Maka anggota himpunan A dan B yang sama inilah yang disebut dengan Irisan. Dengan menggunakan diagram venn maka irisan A dan B adalah sebagi berikut :

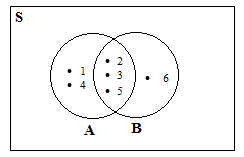
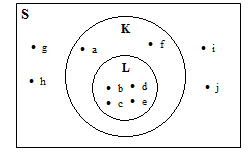
b.    Jika A = {1,2,3,4,5} 

      dan B  = {2,3,5,6}

Maka = {2,3,5}, ditunjukan pada diagram venn berikut :

2. Gabungan Dua Himpunan

Gabungan dua himpunan A dan B adalah semua objek yang merupakan anggota A dan B.

Adapun bentuk umum dari Gabungan adalah :

Contoh :

a.  A = {x │1 ≤ x < 15, x adalah bilangan asli}

B = himpunan bilangan genap yang kurang dari 10

Dari kedua himpunan tersebut kita dapat menyebutkan untuk anggota :

A = {1,2,3,4,5,6,7,8,9,10,11,12,13,14}

B = {2,4,6,8,}

Sedemikian sehingga   = {1,2,3,4,5,6,7,8,9,10,11,12,13,14}

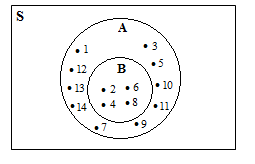
.   S = {a,b,c,d,e,f,g,h,i,j}

K ={a,b,c,d,e,f}

L = {b,c,d,e}

Dari ketiga himpunan tersebut, kita dapat menentukan bahwa KL = {a,b,c,d,e,f}.

Dengan menggunakan diagram venn dapat digambarkan sebagi berikut :

Contoh Soal Diagram Venn

Contoh Soal 1

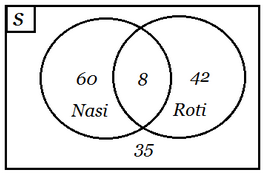
Dalam penelitian yang dilakukan pada sekelompok orang, dipeoleh data 68 orang sarapan dengan nasi, 50 orang sarapan dengan roti, dan 8 orang sarapan nasi dan roti, sedangkan 35 orang sarapannya tidak dengan nasi ataupun roti. Hitung banyaknya orang dalam kelompok tersebut!

Jawab:

Kita gunakan diagram ven untuk menjawab soal tersebut. Jika kita gambarkan dengan diagram ven maka gambarnya seperti gambar berikut ini.

Contoh Soal 2

Dari beberapa anak remaja diketahui 25 orang suka minum susu, 20 orang suka minum kopi dan 12 orang suka susu dan kopi. Dari data di atas jawablah pertanyaan di bawah ini.

a. jumlah semua anak remaja

b. jumlah remaja yang suka susu saja

c. jumlah remaja yang suka kopi saja

d. jumlah remaja yang suka kedua-duanya

Jawab:

Untuk menjawab soal tersebut Anda harus membuat data tersebut menjadi bentuk diagram ven. Jika digambarkan maka bentuk diagram vennya menjadi seperti gambar berikut ini

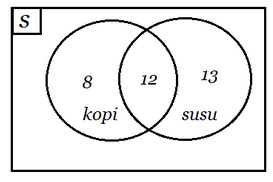
Dari diagram venn di atas maka.

a. jumlah semua anak remaja = 33 orang

b. jumlah remaja yang suka susu saja = 13  orang

c. jumlah remaja yang suka kopi saja = 8 orang

d. jumlah remaja yang suka kedua-duanya = 12 orang

Contoh Soal 3

Hasil survey terhadap 35 orang penduduk di suatu desa, diperoleh hasil sebagai berikut: 18 orang menyukai teh, 17 orang menyukai kopi, 14 orang menyukai susu, 8 orang menyukai minum teh dan kopi, 7 orang menyukai teh dan susu, 5 orang menyukai kopi dan susu, 3 orang menyukai ketiga-tiganya. Buatlah diagram Venn dari keterangan di atas dan tentukan banyaknya warga menyukai teh, menyukai susu, menyukai kopi, dan tidak menyukai ketiga-tiganya.

Jawab:

Diagram Venn dari keterangan di atas seperti gambar berikut ini.

Dari diagram venn di atas maka banyaknya warga yang gemar minum teh saja ada 6 orang, gemar minum susu saja ada 5 orang, gemar minum kopi saja ada 7 orang  dan tidak gemar ketiga-tiganya ada 3 orang.

Contoh Soal 4

Jika diketahui banyaknya kepala keluarga dari warga RT 02 adalah 75 orang. Di antara kepala keluarga ini yang berlangganan koran ada 50 orang, yang berlangganan majalah ada 25 orang, yang berlangganan majalah dan koran ada 10 orang. Dengan menggunakan bantuan diagram Venn, tentukan banyaknya kepala keluarga dari warga RT 02 yang tidak berlangganan keduanya!

Jawab:

Jika digambarkan maka bentuk diagram vennya menjadi seperti gambar berikut ini.

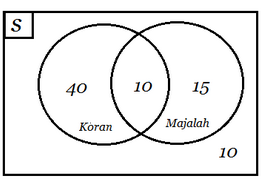
Berdasarkan gambar diagram venn di atas maka banyaknya kepala keluarga dari warga RT 02 yang tidak berlangganan keduanya ada 10 orang.